
| Slide rules HOME page | International | < SITE MAP > |
| What's new |
Gebrauchsanleitung für Taschenrechenschieber
1. Beschreibung
Die Mechanik des Rechenschiebers ist sehr leicht verständlich. Zwei Skalen lassen sich gegenseitig verschieben. Die verstellbare Teilung ist auf der sogenannten "Zunge" aufgebracht. Die jeweilige Einstellung oder Ablesung wird mit dem gleichfalls verstellbaren "Läufer" (eine Glasscheibe mit Haarstrich) vorgenommen.
Die weitaus meisten Rechnungen werden mit oder in Verbindung mit dem Teilungspaar C/D ausgeführt und Sie können Rechenschieber-Rechnen, sobald Sie diese Teilung zu lesen verstehen.
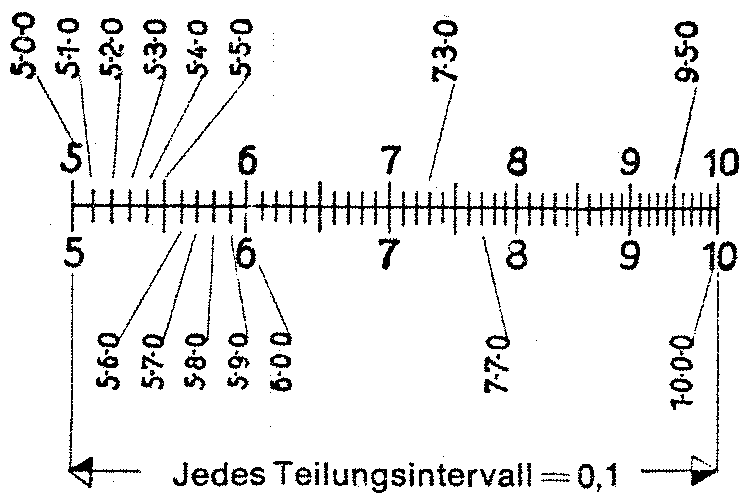
2. Wie wird eine Teilung abgelesen?
Wir bleiben bei dem Teilungspaar C/D. Sie stellen fest, daß die Strecken zwischen den Zahlen am Anfang weiter sind als am Ende der Teilung. Wenn wir alle Unterteilungen zunächst weglassen, sieht sie so aus:

Es ist eir leuchtend, daß es unmöglich ist, die Strecke 9 bis 10 in ebensoviele Intervalle einzuteilen, wie die Strecke 1 bis 2, und Sie erkennen 3 Abschnitte, die sich durch ihre Unterteilungen voneinander unterscheiden.
Allgemeine Anmerkung: Die Nullen bei 10 und 100 sind der besseren Ubersicht halber auf.dem Rechenschieber weggelassen worden.


3. Multiplizieren
Beispiel : 2 x 2,5 = 5 Merkregel: Man multipliziert, indem man Strecken aneinander fügtl
Stellen Sie die 1 der Teilung C über die 2 der Teilung D. Verschieben Sie den Läufer nach 2,5 der Teilung C. Lesen Sie darunter auf der Teilung D das Ergebnis ab = 5.
In dieser Stellung der Zunge können alle Multiplikationen mit 2 abgelesen werden: 2x3=6; 2x4=8; 2x5=10.
Um jetzt weiter mit 2 zu multiplizieren, ist die Stellung der Zunge zu ändern. Die rechte 1 der Zunge muß jetzt über 2 der Teilung D stehen. Nun kann man das Einmaleins mit 2 zu Ende rechnen. Verschieben Sie den Läufer auf 6-7-8-9-10 der Zunge und Sie erhalten auf D die Ergebnisse 12-14-16-18-20.
4. Stellenzahl
Es empfiehlt sich, wenn man sich über die Größenordnung des zu erwartenden Ergebnisses nicht im klaren ist, stets mit abgerundeten Zahlen einen Überschlag zu machen.
Mechanische Kommaregeln haben sich nicht bewährt und sind hier aus diesem Grunde nicht besprochen.
5. Multiplizieren mit Hilfe der Teilung Cl
Wollen Sie das manchmal lästige "Umpolen" der Zunge vermeiden, können Sie auch mit der Teilung Cl multiplizieren. In diesem Fall arbeiten die Teilungen D und Cl zusammen.
Da die Teilung Cl rückläufig aufgetragen ist, bedeuten die Zahlen nicht den angegebenen Wert, sondern stellen deren Kehrwert dar. Die Teilung Cl ist also reziprok zu lesen: die Zahl 5 z. B. bedeutet 1/5
Auf der Teilung C finden Sie jeweils senkrecht darunter den Dezimalwert dazu: Unter Cl 5 finden Sie C 2, das bedeutet 1/5 = 0,2.
Beispiel: 25 x 6= 150
a) Läufer auf D 2-5
b) Stelle die Zunge mit dem Wert Cl 6-0 unter den Läuferstrich
c) Resultat unter Cl 10 (also am Endstrich der Zunge) auf D = 1-5-0.
Eine Überlegung, welcher Endstrich der Teilung zu benutzen ist, entfällt hier, da bei dieser Methode der Endstrich das Resutat anzeigt und einer der beiden Endstriche (CI 1 oder Cl 10) sich stets innerhalb der Teilung D befinden muß.
6. Multiplizieren von mehr als 2 Faktoren
Beispiel: 2,5 x 3 x 8 = 60
Man kann selbstverständlich diese Aufgabe ausschließlich mit dem Teilungspaar C/D lösen. Rationell ist sie aber nur zu lösen, wenn man die Teilung Cl zu Hilfe nimmt.
a) Stelle den Läufer auf D 2-5
b) Bringe Cl 3 unter den Läuferstrich
c) Verschiebe den Läufer nach C 8 und lies darunter auf D das Resultat (= 6).
Vergleichen Sie dagegen die Zahl der Arbeitsgänge, die sich ergeben, wenn Sie nur die
Tellurigen C und D benützen.
7. Dividieren
Merkregel: Man dividiert, Indem man eine Strecke um eine andere kürzt
Man dividiert also mit den Teilungen D und C in genau derselben Art, wie man mit den Teilungen D und Cl multipliziert. Das Resultat wird an einem der beiden Endstriche (C 1 oder C 10) abgelesen.
Beispiel: 475 : 25 = 19
a) Läufer auf D 4-7-5
b) Stelle C 2-5 unter den Läuferstrich
c) Resultat unter C 1 auf D = 1-9.
8. Kettenrechnungen
Wir verstehen darunter Rechnungen, die sich aus kombinierten Multiplikations- und Divisionsaufgaben zusammensetzen.
Beispiel ![]()
Es ist zweckmäßig, zuerst die Division 12,5 : 1,86 durchzuführen, da hierdurch eine weitere Verschiebung der Zunge vermieden wird, wobei das Zwischenresultat garnicht abgelesen wird. Der Läufer wird gleich auf C 6-2-5 gestellt, unter dem Läuferstrich auf D ergibt sich dann das Gesamtresultat.
Die Arbeitsgänge im einzelnen:
a) Läufer auf D 1-2-5
b) Stelle C 1-8-6 unter den Läuferstrich.
c) Verschiebe den Läufer auf C 6-2-5 und lies das Resultat darunter auf D (= 4-2).
Die Stellenzahl ermitteln wir durch Oberschlag mit stark
abgerundeten Zahlen, etwa: 10 X 6 / 2 = 30.
Das Resultat ist auf jeden Fall zweistellig.
9. Die Teilung A/B
Betrachten Sie diese Teilung genau, dann werden Sie sofort erkennen, daß die beiden Hälften 1 bis 10 und 10 bis 100 in derselben Art.eingeteilt sind. Ferner stellen Sie noch fest, daß sich demnach die Teilungen A/B zu C/D maßstäblich wie 2:1 verhalten. Diese Eigenschaft hat man dazu benutzt, auf einfache Weise Quadrate zu bilden, bzw. Quadratwurzeln zu ziehen.
10. Das Quadrat
Beispiel: 15² = 225
Bringen Sie den Schieber in Grundstellung und stellen Sie den Läufer auf C/D 1-5. Lesen Sie unter demselben Läuferstrich auf A/B das Resultat ab = 2-2-5.
11. Die Quadratwurzel
Man verfährt beim Ziehen der Quadratwurzel grundsätzlich umgekehrt wie beim Quadrieren, d. h. man stellt den Radikanden (= die Zahl, aus der die Wurzel zu ziehen ist) auf der Teilung A/B ein und findet die Wurzel auf der Teilung C/D.
Hierbei ist streng zu beachten, in welchem Abschnitt der Teilung die Zahl eingestellt wird.
Merkregel: Streiche von der Zahl von rechts nach links so oft 2 Stellen ab, bis eine ein- oder zweistellige Zahl übrig bleibt. Einstellige Zahlen werden im ersten Abschnitt (von 1 bis 10) der Teilung A eingestellt, zweistellige im zweiten (von 10 bis 100).
Beispiel: ![]()
a) Läufer auf A 2-2-5 (1. Abschnitt)
b) Resultat unter dem Läufer auf D (= 1-5-0).
Beispiel: ![]()
Da hier eine z w eistellige Zahl nach dem Abstreichen übrig bleibt, Ist der Radikand im zweiten Abschnitt von A einzustellen.
Regel für die Stellenzahl: Die Wurzel (das Resultat) hat soviel Stellen, als Gruppen beim Abstreichen entstanden sind.
12. Die Teilung K
Wollen Sie eine Zahl In die dritte Potenz (Kubus) erheben, oder eine Kubikwurzei ziehen, benutzen Sie diese Teilung. Sie arbeitet zusammen mit der Teilung D und steht zu dieser im Verhältnis 1 : 3.
Daß sich hierbei wieder eine Vergröberung der Teilungsintervalle ergibt, ist einleuchtend.
Beispiel: 15,6³ = 3800
a) Läufer auf D 1-5-6
b) Resultat unter dem Läuferstrich auf K = 3-8
Stellenzahl durch Überschlag: 10³ = 1000, also 4-stellig.
Beim Kubikwurzelziehen verfahren Sie ähnlich wie bei der Quadratwurzel, - jedoch streichen Sie statt 2 Stellen jeweils 3 ab.
13. Der Zehner-Logarithmus
Drehen Sie die Zunge um und stellen Sie den Endstrich der Zunge (links oder rechts) auf den gewünschten Wert auf der Teilung D. Die Mantisse lesen Sie dann auf der Teilung L über dem Endstrich der Teilung D ab.
14. Die trigonometrischen Funktionen
Auch für die Ablesung dieser Werte rnüssen Sie die Zunge umdrehen, wobei sich alle Endstriche decken rnüssen. Mit dem Läufer stellen Sie auf S (sin) oder T (tan) die Winkel ein und lesen die entsprechenden Funktionen auf D ab.
15. Der Läufer
Sie haben bisher zu allen Rechnungen den Mittelstrich des Läufers benutzt. Der mit D bezeichnete, halblange Strich gestattet Ihnen nun die häufige Aufgabe, einen Kreisquerschnitt aus dem gegebenen Durchmesser oder umgekehrt, ohne Zuhilfenahme der Zunge, zu bestimmen.
Die Kreisfläche ist: F = ![]()
D² ergibt sich durch den Übergang von dem Teilungspaar C/D zu A/B. Der Faktor p /4 wird dargestellt durch die Entfernung des Läu!ermittelstriches Q zum D-Strich.
Beispiel:: Gegeben: Durchmesser = 22 mm, Gesucht: Querschnitt
a) Stelle den D-Läuferstrich auf D 2-2
b) Resultat unter dem Q-Läuferstrich auf A = 380 mm²